Image compression framework based on conditional diffusion model

Article Information

The paper is titled "Lossy Image Compression with Conditional Diffusion Models" and comes from NIPS 2022. It is the first paper to introduce diffusion models into the field of image compression. Inspired by deep learning-based image coding frameworks and diffusion models, the paper designs a novel image coding framework whose performance can be tuned to perceptual metrics of interest. Experiments show that across multiple datasets and image quality assessment metrics, the proposed model achieves higher FID scores than GAN-based models while remaining competitive with VAE-based models on several distortion metrics. Additionally, training diffusion with parameterization enables high-quality reconstruction with few decoding steps, significantly enhancing the model's practicality.

Abstract

This paper outlines an end-to-end optimized lossy image compression framework using diffusion generative models. The method relies on a transform coding paradigm where images are mapped to an entropy-coded latent space and then back to the data space for reconstruction. Unlike VAE-based neural compression, where the (mean) decoder is a deterministic neural network, the decoder here is a conditional diffusion model. Thus, the approach introduces an additional "content" latent variable that conditions the reverse diffusion process and stores image information. During decoding, the remaining "texture" variables characterizing the diffusion process are synthesized. The paper demonstrates that the model's performance can be tuned to perceptual metrics of interest. Extensive experiments across multiple datasets and image quality metrics show that the method achieves higher FID scores than GAN-based models while remaining competitive with VAE-based models on distortion metrics. Moreover, training diffusion with X-parameterization enables high-quality reconstruction with few decoding steps, greatly enhancing the model's practicality.

Contributions

(1) A novel transform coding-based lossy compression scheme is proposed. The method uses an encoder to map images to contextual latent variables, which then serve as inputs to a diffusion model for reconstruction. The approach can be modified to enhance specific perceptual metrics.

(2) The model's loss function is derived from a variational upper bound of the implicit rate-distortion function of diffusion models. The resulting distortion term differs from traditional VAEs by capturing richer decoding distributions. Furthermore, it achieves high-quality reconstruction with only a few denoising steps.

(3) Extensive empirical evidence shows that variants of the method often outperform GAN-based models in perceptual quality (e.g., FID). The base model also demonstrates rate-distortion performance comparable to MSE-optimized baselines.

Problem Definition

In the transform coding approach to image compression, an encoder uses a parametric analysis transform g_a(x; φ_g) to convert an image into a latent representation y, which is then quantized to form ŷ. Since ŷ is discrete, it can be losslessly compressed using entropy coding techniques (e.g., arithmetic coding) and transmitted as a bitstream. The decoder recovers ŷ from the compressed signal, dequantizes it, and applies a parametric synthesis transform g_s(ŷ; θ_g) to reconstruct the image x̂. Here, g_a and g_s are general parametric functions (e.g., artificial neural networks) rather than linear transforms used in traditional compression. The parameters θ_g and φ_g encapsulate weights such as those of neurons. The problem is thus defined as follows: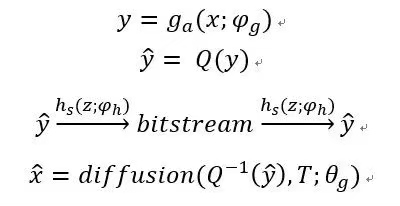

Method

5.1 Model Overview

The figure below illustrates the proposed model. The encoder first transforms the image into a discrete "content" latent variable z, which contains image information. During decoding, this variable guides the denoising diffusion process to reconstruct the image.

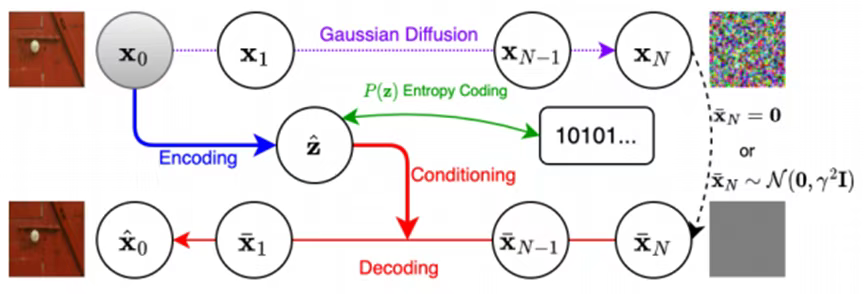
The encoding process is as follows: First, the image x is encoded into its latent representation y = Evae(x). Then, y is quantized. Finally, z is entropy-coded for storage or transmission.

During decoding, Gaussian noise is randomly generated while inverse quantization computes ŷ = Q^(-1)(z, γ). ŷ then serves as contextual guidance for the Gaussian denoising process, which recovers the reconstructed image x after t denoising steps. The full encoding/decoding process is outlined in the algorithm below:

5.2 Encoder

The paper does not specify the encoder's network architecture, which could be any feature-extracting network (e.g., fully connected or convolutional networks).

5.3 Decoder

The decoder is based on a conditional denoising process. First, a set of random Gaussian noise is generated, and the image is reconstructed through t denoising steps. Each step takes the previous denoising result as input, guided by the denoising count t and the context vector. The denoising network employs a classic U-Net architecture.

5.4 Hyperprior Network

The paper uses a joint context and hierarchical entropy model to encode quantized latent signals into a bitstream. These models are well-studied in literature. Entroformer is chosen as the entropy model due to its superior experimental performance. It consists of a transformer-based hyperprior and a bidirectional context model to estimate the distribution P(z) of latent functions and encode them into a bitstream via arithmetic coding.

5.5 Conditional Diffusion Model

The foundation of the compression method is a novel latent variable model: the diffusion variational autoencoder. It has a "semantic" latent variable z for encoding image content and a set of "texture" variables x1:N describing residual information. The decoder follows a denoising process conditioned on z.

Experiments

A large-scale compression evaluation was conducted, involving multiple image quality metrics and test datasets. Beyond traditional distortion metrics, perceptual quality metrics were also considered. Some metrics are fixed, while others are learned from data.

Sixteen image quality assessment metrics were selected, with eight widely used ones detailed in the paper. Notably, recent learned metrics better capture perceptual attributes/realism than non-learned methods; these are labeled as perceptual metrics, while others are distortion metrics. For FID calculation, images were split into non-overlapping 256×256 patches following Mentzer et al. (2020).

The figure below illustrates the rate-quality trade-off on the DIV2K dataset. The X-prediction model requires only 17 decoding steps, far more efficient than ϵ-prediction models needing hundreds of steps for comparable performance. Dashed lines represent baseline models, while solid lines denote the proposed CDC model. The eight plots distinguish two metric types by their frame colors.

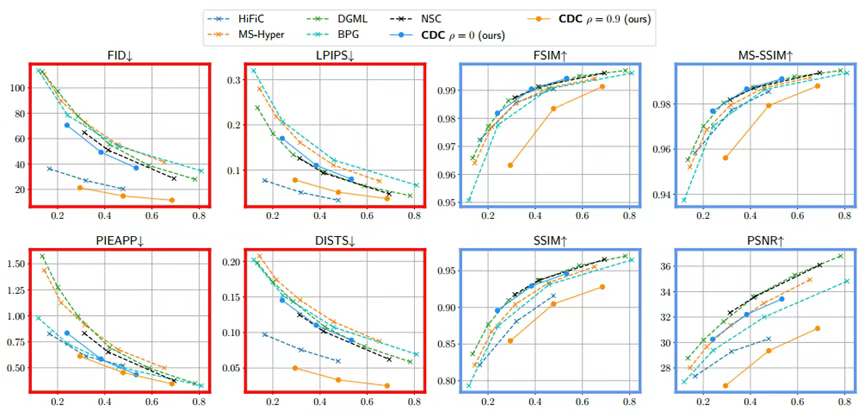
The proposed CDC(ρ=0) and CDC(ρ=0.9) exhibit qualitative differences in perceptual and distortion metrics. Setting ρ=0 optimizes only the bitrate-diffusion loss trade-off, outperforming ρ=0.9 on model-based distortion metrics (except PSNR). Qualitatively, decoded images show fewer over-smoothing artifacts compared to VAE-based codecs. Conversely, CDC(ρ=0.9) excels in perceptual metrics. Adjusting ρ enables control over the three-way trade-off between distortion, perceptual quality, and bitrate.