Principles of Image Compression (with a small amount of linear algebra popularization)

Wavelet Basis-Based Compression Algorithms

All compression algorithms mentioned here are lossy compressions.

It is believed that everyone understands that images are represented in computers as pixel matrices (i.e., the so-called bitmaps; of course, vector graphics also exist, but most images we encounter in daily life are bitmaps).

The JPEG, PNG, and GIF formats that everyone uses every day are actually compressed image formats. Their underlying data does not record the RGB values of each pixel one by one. In contrast, the format that truly does this is probably the BMP format, which everyone is more familiar with (it contains genuine raw data that has never been compressed). This is why BMP images of the same specification are usually much larger than JPEG images. So today, we will talk about how to compress the "raw data that records pixel RGB values".

Let’s discuss the simplest scenario: if I show you a pure white image or an image with only one color, how would you compress it? It’s very simple—you just need to provide the color information of that color and tell the computer that all pixels in this image are of that color. This compression method does not cause any loss of image details (or rather, such images have no details in the first place) and has an extremely high compression ratio. However, in daily situations, our images are not like this. This compression method would erase all details of the image, resulting in a uniformly gray picture in the end.

So, what if we make some compromises by dividing the image into small blocks and then applying this algorithm to each small block? It sounds somewhat familiar, doesn’t it?

That's right, in essence, mosaic is also a type of lossy image compression algorithm.

Yes, although the purpose of pixelation (adding mosaics) is not to compress images, from an algorithmic perspective, mosaics are indeed a form of lossy compression for images. This is why it’s said that removing mosaics is harder than climbing to the sky—vast amounts of information are lost during the process of adding mosaics.

It’s like if you give me two numbers, I add them together to get 10, and then I tell a third person that I have two numbers that add up to 10. If I don’t tell them either of the numbers, it’s impossible for them to 还原 (recover) the original two numbers.

If we delve deeper from the perspective of information theory, this seems to involve principles like entropy increase, but we won’t go into that here.

Most of the images we encounter in daily life can be approximately viewed as consisting of solid-color patches in their local areas. For example, a stretch of blue sky or sea, large expanses of snow, the blackboard in a classroom, or an asphalt road—these are all places where large solid-color blocks repeat over and over again.

In that case, this area must contain a great deal of highly similar color data, which creates the possibility for compression. A natural thought arises: Can we replace these large amounts of repeated data with a small amount of non-repetitive data, while make the best to not damaging the details of the image? This is essentially a basic idea behind image compression. Now, let’s start talking about how to implement it.

First, we have the pixel information carried by the image. To compress it, a natural question is: Can we discard some of this information in some way? For now, we can’t, because each coefficient here represents the grayscale value of a pixel—removing any one of them would leave that pixel completely black. So how can we make some data "worth discarding"?

The answer is to process this data in a way that makes some parts carry more information (in a loose sense, meaning they have a greater impact on the image’s appearance) and others carry less. A group of researchers came up with an ingenious method:

First, we split the image into 8x8 small blocks, flatten each block into a single row, and then place these 64 grayscale values into a 64-dimensional vector. Don’t think this is something fancy—you don’t need to imagine what a 64-dimensional space looks like (no one can, anyway). Just know it’s an array with 64 numbers. It has no essential difference from 2D or 3D vectors except that it is longer in length. That’s all there is to it.

Here, we have to introduce an extremely important concept in linear algebra: a set of vectors that can span a space. We call them... [High energy ahead] "basis" [Fujoshi fans, please wipe away your drool].

To understand what a basis is more intuitively, let’s take an example: When we look at a vector, what do the numbers in it represent? They represent...

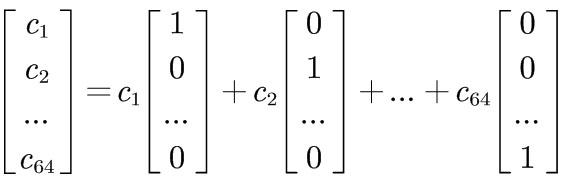
In fact, what they represent is the "linear combination" of the standard basis using these numbers.

Don’t be intimidated by this fancy term. It simply means taking several times of this, plus several times of that, plus several times of...

It’s essentially no different from buying two catties of Chinese cabbage, one catty of celery, and three catties of eggplant when shopping for groceries.

In that case, we can say that what you bought today is a linear combination of Chinese cabbage, celery, and eggplant.

See? It’s really simple.

(Pardon me for using this example; I just wanted to tease those "math is useless" advocates who claim that "learning calculus is pointless for buying groceries.")

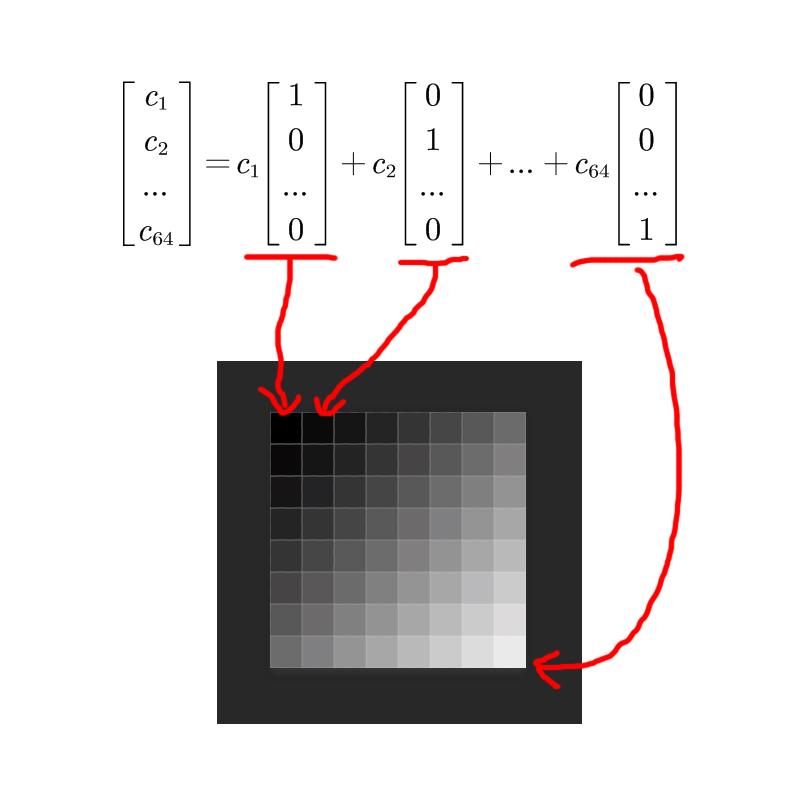
Then, what does a basis vector here represent?

Exactly—it represents the grayscale value of one of the pixels.

So each number here has an equal status.

Now, we want to expand it onto another set of bases (basis transformation is an extremely important component in image compression; different compression algorithms use different bases, and the wavelet basis here is just one of them).

What does "expansion" mean?

Simply put, it is to decompose (represent) a vector into a linear combination of a set of bases.

Naturally, an n-dimensional vector needs a set of n vectors as a basis for its representation.

What you just saw is the expansion of a vector onto the standard basis, like this:

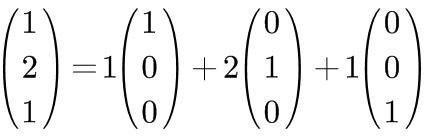
For the same vector, you can also expand it onto [1,1,1], [0,1,1], and [0,0,1].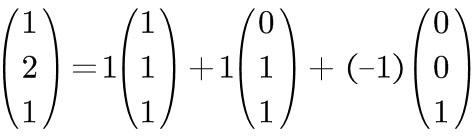

Or onto [1,1,0], [0,1,1], and [1,0,1].

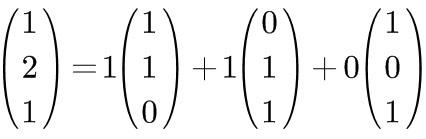
For the same vector, you can also expand it onto [1,1,1], [0,1,1], and [0,0,1].

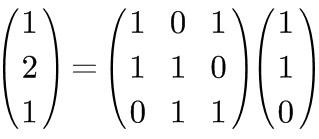
So how do we expand a given vector onto a specific set of bases?

A sophisticated way to put it is to left-multiply by the inverse of the basis matrix.

The inverse of a matrix is somewhat similar to the reciprocal of a number.

Like this: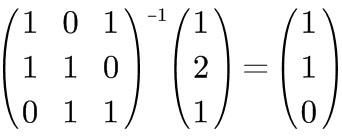

The vector obtained on the right side of the equation is the result of the original vector under the given basis transformation.

What we will store later is precisely this vector obtained on the right side.

When reading a compressed file, it can be restored simply by left-multiplying by the original matrix itself;

Like this:

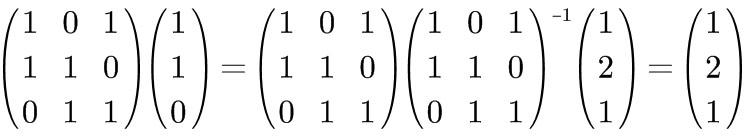
Simple, right?

Let’s go back to the vector obtained after basis transformation.

For vectors under the standard basis, these numbers are equally important. With such a vector, discarding any one of the numbers will cause the pixel at that position to turn completely black.

So, is there a set of bases such that when an image is represented under these bases, some numbers are more important than others—important enough that discarding the less important numbers still allows the image to roughly retain its original form?

Yes, wavelet bases are precisely such a thing.

Note that this is just a simplified version; the waves used in practice are much smoother than this.

Please take a moment to stare quietly at this matrix for 5 minutes.

Have you found the pattern?

Of course, what I’m showing you here is an 8th-order wavelet basis matrix. To expand a 64-dimensional vector, a 64-dimensional matrix is needed.

"But teacher, what does a 64-dimensional wavelet basis matrix look like?"

Well, a 64-dimensional wavelet basis matrix looks like this.

Isn’t it quite pleasing to the eye?

Alright, originally our file needed to store 64 numbers, and now we still need to store 64 numbers. But—but—but here comes the exciting part:

Under the standard basis, all numbers are "equal".

Yet under the wavelet basis, these numbers are assigned a hierarchy— the earlier numbers are far more important than the later ones.

This allows us to compress the image by discarding those dispensable later numbers. Among these new 64 numbers, only a small portion plays a crucial role in our image. These vital numbers are placed at the front of the vector, while the insignificant ones are at the back. Why is that?

Let’s go back and observe what happens when this vector is left-multiplied by the wavelet basis matrix.

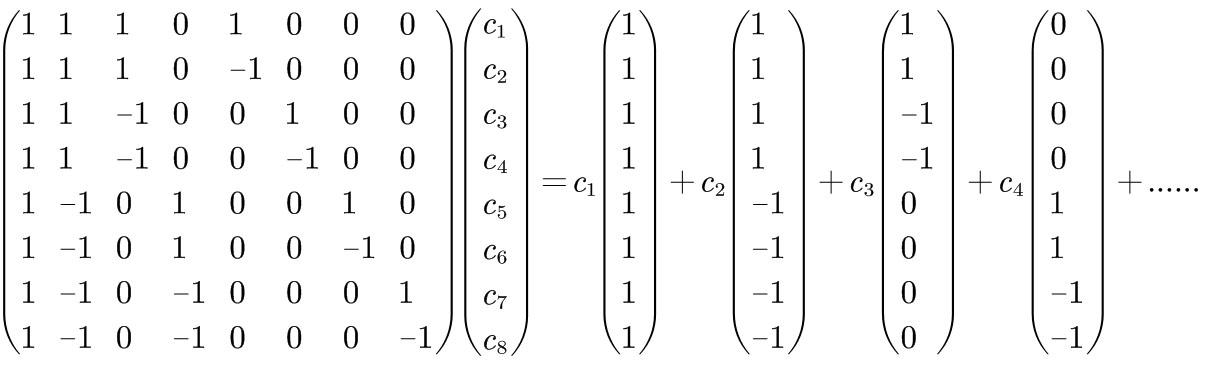
I wonder if everyone can tell: the first number sets the overall tone of the entire region.

The second number divides the region into two parts and represents the difference between them.

The third and fourth numbers further split each of the previous two parts into two again, and indicate the differences within these new divisions. And so on.

Have you noticed? This is a progressive relationship from the macro to the micro, from the general to the specific, and from the overall to the local.

To put it in simpler terms:

The first number of this vector sets the basic tone of the entire image.

The second number adds some rather rough information.

The second to fourth numbers add more details that are still rough but less so than the previous ones.

The fifth to eighth numbers add even finer details. And this pattern continues.

If we want to represent all the details of an image, we must use every component of the resulting new vector. However, in that case, the image wouldn’t be compressed at all.

Yet, in many cases, when we discard the numbers that represent trivial, minute details, our naked eyes can barely notice the difference (we can just fill them with zeros during decompression).

For example, if we remove the coefficients of vectors that only have values like 1 or -1 (which represent the finest details) while the rest are zeros, the image size will be reduced to half of its original.

If our image blocks are similar to the ones mentioned earlier—like patches of sky, snow, or sea, which are close to solid colors but not entirely pure—

the coefficients obtained when expanding them onto wavelet bases will mainly concentrate in the low-frequency part at the front, with only scattered small coefficients in the high-frequency part at the back.

Removing these high-frequency coefficients will hardly affect the image.

So this is the entire process.

Here is an uncompressed image.

There is also an image compressed to 1/2 of its original size.

There is also an image compressed to 1/4 of its original size.

If you don’t look very carefully, it’s still not easy to notice the difference.

Under what circumstances will this algorithm not cause loss to the image?

Think about it.

The natural answer is: when the image vector is expanded onto the wavelet basis, the coefficients we plan to remove happen to be zero.

To put it in a more sophisticated way: there are no high-frequency components.

And under what circumstances will this algorithm cause the maximum loss of image details?

This is a very tricky question. Let’s think carefully about what the numbers we discard determine.

It can be roughly understood as the difference between adjacent pixels and the highest-frequency color differences.

So, suppose we take a checkerboard-patterned image and feed it into our algorithm for compression. What result will we get?

First of all, the overall tone of the entire image is gray with a value of 128—this goes without saying, and everyone can figure that out, right?

What will be left after we remove this base tone from the image?

An image with alternating +128 and -128 values (this is not strictly accurate because pixel values cannot be negative, but you get the idea).

In other words, all that remains is the highest-frequency information, which is exactly what we will discard.

Therefore, such a checkerboard image, after compression, will result in a pure gray image.

And common sense tells us that if you look at a black-and-white interleaved image from a distance, what you see should be a patch of gray.

So the worst-case scenario (with the maximum information loss) is no more than this. (Everyone: Wait, what do you mean by "no more than this"? This loss is already significant, okay?)

To summarize in one sentence: Keep the low frequencies, filter out the high frequencies; retain the large details, remove the small details.

Finally, it should be stated that this is only the most basic and core idea of image compression. Truly mature compression algorithms are much more complex and achieve far better results (both in terms of image quality and compression ratio).

A real JPEG can easily achieve a 1/20 compression ratio without visible loss.